Vous connaissiez peut-être les plaques Herbinière-Lebert assemblables à l’aide desquelles les élèves peuvent composer et décomposer les premiers nombres dès l’école maternelle. Elles ont été revalorisées par Rémi Brissiaud pour construire les nombres comme « relations entre des quantités » et les modernes plaques Numicon ont pris leur suite.

Découvrez à présent d’autres plaques (dessin en bas à droite)  créées par Suzanne Herbinière-Lebert en 1923 : les « plaquettes trouées avec éléments mobiles ». Elles avaient disparu après la guerre mais je les ai redécouvertes dans les documents d’époque et utilisées avec profit dans ma classe en utilisant des situations proposées par leur créatrice pour construire les premiers nombres. Je propose aussi de nouvelles situations permettant d’organiser mentalement n’importe quelle collection en s’appuyant sur cette collection-témoin organisée.

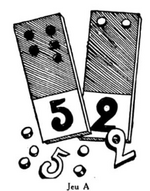
 Jeux B et A de Suzanne Herbinière-Lebert créés en 1923 et édités en 1931.

Le jeu B (à gauche) est aussi nommé « plaquettes en relief avec éléments fixes ».

Le jeu A (à droite) est aussi nommé « plaquettes trouées et chiffrées avec éléments mobiles ».

Voici deux vidéos en exemple avant d’aborder l’article plus développé que vous pouvez aussi télécharger ici

.

Lire la suite...

Voici le bilan de mes longues recherches sur les formes et usages d'un matériel français largement oublié, qui revit aujourd'hui avec notamment le britannique Numicon : les « Plaquettes pour l'initiation sensorielle au calcul » créées en 1923 par l’institutrice Suzanne Herbinière-Lebert (1893-1985).

J'ai retrouvé leurs origines et leurs cousines proches en Allemagne depuis 1867, leurs transformations, et leurs enjeux pour servir la construction du nombre comme "relation entre les quantités" revalorisée par le regretté Rémi Brissiaud qui s'inscrivait dans une grande tradition française, celle de Buisson, Châtelet et Mialaret, éclipsée par les "mathématiques modernes" dans les années 1960 puis par le "comptage-numérotage" à partir de 1986 jusqu'à ce que les programmes de la maternelle et de l'élémentaire la retrouvent à partir de 2015.

Ce large inventaire historique se frotte aussi à des matériels aux objectifs proches : les "constellations" du dé, les "images-nombres" de Lay (qui eurent une importance considérable au début du XXe siècle) et les "grilles de 10" qui dominent dans de nombreux pays.

Je propose aussi des situations d'apprentissage éprouvées dans ma classe de maternelle.

L'originalité profonde et l'intérêt des plaquettes Herbinière-Lebert sont les suivants :

• Ce sont d’abord les seules collections-témoins organisées (avec dans une moindre mesure celle de Lay appuyées sur le repère 4) qui permettent de représenter toutes les décompositions des 10 premiers nombres sans « jamais remanier le précédent groupement pour obtenir le nouveau », (Abbadie). Chaque représentation d’une quantité est ainsi clairement et régulièrement formée à partir des précédentes, véritablement mise en relation grâce à des situations d’apprentissage adéquates, ce qui permet aux élèves de construire des représentations des nombres plutôt que de seulement mémoriser des organisations de points dans l’espace.

• Pour cette raison ce sont aussi les seules collections-témoins organisées de manière non-linéaire qui peuvent représenter chaque quantité comme un tout manipulable (les plaquettes) : ces collections peuvent être jointes (et disjointes en passant par un échange) pour composer ou décomposer une quantité, sans besoin de déplacer chaque unité et de compter 1 à 1 au risque du numérotage.

Télécharger ici les 177 pages abondamment illustrées

  de :

Gonzague Jobbé-Duval, "Les plaquettes Herbinière-Lebert (1923). Born (1867), Schneider (1899), Brissiaud (1989), Numicon (1996) et au-delà, enquête sur une collection témoin organisée de manière à construire les nombres comme "relations entre des quantités", A tâtons, http://goupil.eklablog.fr/les-plaquettes-herbiniere-lebert-1923-origines-concurrents-et-enjeux-a-a207526198

*

Vous pourrez aussi être intéressé.e par mon article sur : "Les "Noums" de Rémi Brissiaud, ancêtres et enjeux". A tâtons, http://goupil.eklablog.fr/les-noums-de-brissiaud-ancetres-et-enjeux-a175398670

Il brosse le tableau de la plupart des outils de la famille des réglettes Cuisenaire.

Lire la suite...

Les « Plaquettes Herbinière-Lebert pour l'éducation sensorielle et l'initiation sensorielle au calcul » furent créées en 1923 par l’institutrice Suzanne Herbinière-Lebert (1893-1985), qui devint Inspectrice générale de l’Instruction publique. Diffusées largement pendant cinquante ans, elles disparurent dans les années 1970 avec les « mathématiques modernes ». Rémi Brissiaud promut à nouveau les plaquettes Herbinière-Lebert à partir de 1989 et leur principe survit dans certains de ses Albums à calculer pour la maternelle ou dans ses manuels pour l’école élémentaire quand les élèves comptent « comme Perrine », mais le matériel concret en lui-même s’est éteint et sa créatrice, qui fit rayonner l’école maternelle française à l’étranger, ne fait plus l’objet que de brèves mentions.

Les origines de ces plaques sont encore davantage oubliées : quelques chercheurs se souviennent que leurs configurations viennent de l'Allemand Born (1867) et je relate ici comment j'ai découvert que les premières plaquettes à l'usage du maître d'école ont été créées par un autre Allemand : Georg Schneider, autour de 1900. Ce dernier critique déjà ce que le regretté Rémi Brissiaud appelait plus récemment le "comptage-numérotage".

Lire la suite...

Ce Padlet a d'abord été élaboré pour mes élèves de maternelle confinés et leurs parents afin d'aborder les nombres comme relations entre des quantités.  Je mets en valeur les stratégies de décompositions-recompositions des nombres favorisées par le programme depuis 2015 et mises en avant de longue date par Rémi Brissiaud. Mes vidéos de marionnettes illustrent les "premiers dialogues" préconisés par Rémi Brissiaud dans
Premiers pas vers les maths. Les chemins de la réussite à l’école maternelle, Paris : Retz, 2016, 95 pages.  Ce padlet emprunte aussi plusieurs vidéos ou autres media dont je ne suis pas l'auteur.

Des élèves de moyenne section, voire de grande section, qui auraient besoin de reprendre les bases trouveront aussi ici du grain à moudre.

Une version rédigée de ce padlet (et qui propose aussi d'autres situations jusqu'à la grande section) se trouve dans un autre article du blog.

Lire la suite...

Zbigniew Antony Lubienski / Roland Wentworth Lubienski, époux de la pédagogue Hélène Lubienska   de Lenval, améliore le système de perles en base 10 de Maria Montessori  avec des cubes en bois. Disciples proches et principaux collaborateurs du seul cours international Montessori qui ait eu lieu en France, les deux époux perdront la faveur de la dottoressa.

Lire la suite...

Lire la suite...

Un matériel visant à aider l’enfant à comprendre le système décimal et la numération de position avec des cubes, des plaques carrées, des barres et des cubes-unités circule aujourd’hui sous différents noms. Deux auteurs sont parfois mentionnés – Zoltan Pal Dienes, Hélène Lubienska – et une grande ancêtre : Montessori. Mais en remontant les sources, je suis arrivé à Heer en 1836 qui eut de nombreux successeurs. Quant à Dienes, dernier venu, plutôt que de simplement illustrer le système décimal pour faciliter les opérations, il mit plutôt l'accent sur d'autres bases que 10 pour mettre les enfants en situation de recherche et leur permettre d'atteindre une "vue d'ensemble des propriétés élémentaires des nombres".

Lire la suite...

Voici des défis scientifiques proposés par la fondation La main à la pâte et d'autres ressources qui peuvent être utiles aux familles pendant le confinement.

Lire la suite...

Bonjour, je* m'appelle ​Christian Voltz. J'écris et je dessine des livres. Aujourd'hui je te propose un défi bricolage : construire un personnage à ma manière.

Lire la suite...

Au fabuleux Musée de la musique et avec le conte musical Pierre et le loup.

Lire la suite...

100 pistes publiées sur l'espace numérique de travail (ENT) en attendant la reprise de ma classe de moyenne et grande section de maternelle.

Elles ne prétendent pas permettre la "classe à la maison" ni assurer une réelle "continuité pédagogique" mais donner des pistes à qui voudra s'en saisir... Ou pourra s'en saisir car, même si j'ai fait l'effort de réaliser quelques vidéos très accessibles, je sais que toutes les familles ne sont pas également armées pour mettre à profit mes activités qui demandent souvent du temps, une certaine maîtrise des codes et des priorités de l'école, une familiarité avec le type de culture valorisé par l'école. Et une classe c'est aussi un collectif et une maîtresse / un maître. Bref, voici un ersatz de classe mais le voilà tout de même.

Lire la suite...

Le but du jeu est d’amener tous les disques (3 ou 4 disques dans le cas d'un enfant de maternelle) en un minimum de coups de la tige de gauche à la tour de droite. Il y a 3 tiges. Les disques sont de plus en plus petits en partant du socle. Les règles de déplacement sont les suivantes :

• On déplace un seul disque à la fois.
• On place un disque seulement sur une place vide ou sur un disque plus grand que lui.

Lire la suite...

Cet article a d'abord été élaboré pour mes élèves de maternelle confinés et leurs parents. Vous trouverez ici des pistes d'activité de la petite à la grande section pour comprendre les nombres comme relations entre des quantités.  Je mets en valeur les décompositions-recompositions des nombres favorisées par le programme depuis 2015 et les "collections témoins organisées" ou "nombres figuraux" mis en avant par Rémi Brissiaud. C'est à ce dernier que je dois ma formation sur le sujet et je lui emprunte tout le début de l'article (premiers dialogues, etc.) J'apporte une contribution personnelle dans mes vidéos dédiées aux enfants et dans la description de 6 jeux de décomposition.

Lire la suite...

Voici une description personnelle d'un grand jeu de décomposition des nombres popularisé dans les écoles par Alice Descoeudres puis Rémi Brissiaud.

Objectif d’apprentissage : décomposer les nombres de 1 à 10.

But du jeu : trouver combien de jetons/cailloux…  sont cachés sous le gobelet en s’appuyant sur la quantité totale vue au départ et celle qui reste visible à côté du gobelet.

Lire la suite...

 À l’occasion de la visite du ministre de l’éducation de Singapour dans une classe française expérimentant sa nouvelle méthode de compréhension des nombres, Rémi Brissiaud évoquait ses sources d’inspiration  : « Sur le Facebook du ministre, Les Noums-CP est présenté comme s'inspirant de la méthode de modélisation de Singapour. Oui, mais il ne faut pas oublier que nous nous inspirons également des nombres en couleurs de Cuisenaire et, évidemment, de Picbille. »

Pour bien comprendre je suis revenu aux sources mentionnées par Rémi Brissiaud mais aussi à la grande histoire des barres/réglettes/tiges de calcul depuis Ernst Tillich en 1806 et j’ai découvert plusieurs ancêtres qui avaient les mêmes objectifs : initier aux nombres comme relations entre des quantités. Chaque matériel avait son originalité et, au moins pour une part, sa pertinence. Nous verrons ce que changent les choix de Brissiaud et les possibilités d’un logiciel informatique.

Télécharger le fichier PDF ici

Lire la suite...

J’introduis mes élèves de moyenne et grande section de maternelle à des jeux traditionnels abstraits pour deux joueurs qui permettent de travailler la notion d’alignement et favorisent la recherche de stratégies.

Cette activité prend tout son sens si les règles et stratégies sont verbalisées par les élèves.

J’ai réuni les jeux en quelques catégories. En maternelle il est sans doute nécessaire de ne présenter qu’une ou deux catégories car le coût d’acquisition des règles et stratégies est important chez des élèves non lecteurs. Il me parait judicieux d’explorer chaque catégorie avant de passer à la suivante et au sein de chaque catégorie d’introduire les jeux par ordre de difficulté.

Lire la suite...

J'apprends cette année à mes élèves de moyenne et grande section de maternelle trois poèmes de Guillevic (1907-1997) :

• « Un marteau » (Sphère, Gallimard, 1963)

•  « Rocher » (Sphère, Gallimard, 1963)

• « Ma girafe et moi »(Autres, Gallimard 1980)

Lire la suite...

Rémi Brissiaud, jugeait en 1989 que les anciennes leçons proposées avec les plaques-nombres rendaient les élèves « très dépendants de l’adulte, tant dans la gestion de l’activité que dans son évaluation »¹.

Il souhaita donc faire de ce matériel un « outil de communication dans la relation maître-élève ». En 1994, dans un Livre du maître pour la grande section de maternelle², il proposait des activités « ludiques » en ce sens et expliquait comment fabriquer le matériel Herbinière-Lebert avec du carton. Il développait aussi par ailleurs des « Livres à calculer » qui s’appuient sur les configurations Herbinière-Lebert (ou bien sur celles du dé reconfigurées par ses soins).

Voici les situations préconisées par Brissiaud³ en 1994

Lire la suite...

J'entraîne les élèves de maternelle (moyenne et surtout grande section) à la décomposition des nombres 2 à 10 en privilégiant ici deux types de décompositions : 5+n et n+1. Je m'appuie sur des dés reconfigurés pour forcer l'entrainement à ces décompositions. Voici comment et pourquoi. 

Lire la suite...

Vous connaissez sans doute les "grilles de 10", ces grilles de 10 carrés que nous appelons souvent en France les « cartes à points ». On les confond souvent avec les configurations Herbinière-Lebert. Il faudrait pourtant les distinguer par la disposition respective des points, par leurs dates de création et par leurs usages distincts.  

Les grilles de 10

Lire la suite...