Pourquoi cette exposition au Musée de l'école (Chartres) ?

Une exposition raisonnée de matériels d’enseignement élémentaire des mathématiques est chose très rare. L’excellent Musée national de l’éducation (Munaé, à Rouen) par exemple, n’a encore consacré à ce thème aucune de ses 120 expositions temporaires. Peut-être parce qu’il n’existe pas de synthèse universitaire sur l’histoire de ces matériels et très peu d’études particulières en dehors de celles concernant le boulier.

Par ailleurs la « décomposition des nombres » et l’étude de leurs « relations internes » - sont revenues au programme de nos écoles dès la maternelle depuis 2015 après une éclipse de 45 ans. L’exposition eut pour titre provisoire : « Les nombres en relations ».

Enfin 2023 est le centenaire des « plaquettes d’initiation sensorielle au calcul », créées par l’ancienne inspectrice générale Suzanne Herbinière-Lebert, qui retrouvent le chemin des classes depuis quelques années sous d’autres noms (particulièrement le britannique "Numicon"). Le Musée de l’école en expose un très rare ensemble.

Quel bilan ?

L’exposition, au Musée de l’école de Chartres et d’Eure-et-Loir, de matériels d’enseignement élémentaire des mathématiques, a permis de mettre en lumière plusieurs stratégies pour construire les premiers nombres en étudiant leurs relations et de présenter des situations d’apprentissage.

De nombreux concepteurs occidentaux de matériel didactique ont, dès le début du 19^e siècle, choisi de représenter géométriquement la relation fondamentale de l’itération de l’unité par des points alignés, parfois matérialisés par des boules ou des cubes.

Cette représentation se heurte à une obstacle pratique : celui de notre capacité à  évaluer par un jugement rapide, précis et confiant une collection quelle que soit sa configuration (ce que nous appelons « subitisation » depuis 1949). Cette capacité d’évaluation est très bonne jusqu’à seulement 3 objets d'après J.-P Fischer (mais d'anciens pédagogues pensaient qu'elle pouvait aller jusqu'à 4 voire 5 objets). Les élèves en sont donc souvent réduit à compter 1 à 1 au risque de numéroter les objets en récitant la comptine comme un alphabet, sans comprendre les diverses relations internes aux nombres.

Les pédagogues présentés dans cette exposition ont trouvé comme solution de constituer les boules en groupes colorés de 2, 3, 4 ou 5, voire d’empêcher la manipulation des boules une à une pour favoriser la manipulation des collections elles-mêmes en enfilant les boules hors du boulier en barrettes ou en les remplaçant par des cubes regroupés en barres insécables afin de s’appuyer sur l’analogie de la longueur.

Ces stratégies n’empêchant pas entièrement le comptage un à un, des pédagogues optèrent pour l’attribution conventionnelle d’une couleur à chaque quantité et/ou éliminèrent toute séparation entre les unités de base afin de favoriser la découverte des relations entre chaque quantité validée par la comparaison des longueurs, au risque cette fois de rendre plus difficile l’accès aux quantités discrètes pour les plus jeunes ou plus faibles élèves.

 Concernant cette option des couleurs pour les barres et perles ou pour les plaques, rappelons que les attributions de couleurs sont conventionnelles (3 n’est pas plus jaune que bleu) et qu’elles peuvent tout au plus symboliser par convention telle ou telle relation entre les quantités (doubles et moitiés, relations factorielles…) si on regroupe certaines représentations des nombres par des teintes apparentées.

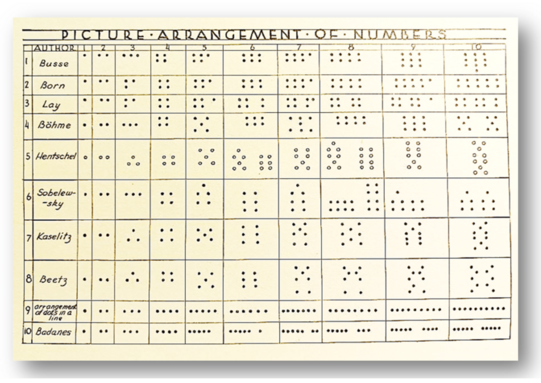
D’autres pédagogues choisirent de renoncer à l’alignement des unités, au profit d’une organisation dans l’espace qui tient compte de la capacité de subitisation. Ces représentations fondées sur les repères 2, 3, 4 ou 5 (ou sur une combinaison de ces derniers) permettaient de construire chaque représentation d’un nombre à partir d’autres et, par exemple d’évaluer, sans compter un à un, les 5 points du dé par les décompositions 2 + 3 ou 4 + 1.

Certaines de ces représentations manifestent le choix de privilégier des regroupements le plus proche de 3 (limite de subitisation), d’autres mirent en valeur pour chaque représentation de nombre les décompositions les plus aisées ou les plus utiles pour le calcul, d’autres essayèrent de s’approcher au maximum de la rigoureuse représentation géométrique de la suite des nombres entiers (qui est celle des représentations alignées) en s’efforçant de « jamais remanier le précédent groupement pour obtenir le nouveau » (Abbadie).

Un seul type de représentation le permit  : celui de Born, connu en France sous le nom d’Herbinière-Lebert, qui représenta systématiquement chaque quantité comme clairement et régulièrement formée à partir des précédentes, permettant ainsi aux élèves de manipuler les collections elles-mêmes pour limiter le comptage[1] 1 à 1 et de valider visuellement un résultat anticipé mentalement (par exemple, pour recouvrir une plaque de 8 je peux mettre bout à bout une plaquette de 3 et une plaquette de 5 ou bien 6 et 2, etc.).

Pour lire le parcours complet de l'exposition et les analyses approfondies, téléchargez ce document ou visionnez-le ci-dessous.

Je peux faire parvenir, sur demande, une version avec de meilleures photos.